You'll find said tool on my GitHub repository - https://github.com/cyclaero/xcssecovid
Quick Start
What the hell is a Logisitc Function?
According to Wikipedia - https://en.wikipedia.org/wiki/Logistic_function:
A logistic function or logistic curve is a common "S" shape (sigmoid curve), with equation:

The logistic function finds applications in a range of fields, including artificial neural networks, biology (especially ecology), biomathematics, chemistry, demography, economics, geoscience, mathematical psychology, probability, sociology, political science, linguistics, and statistics.
As a matter of fact it is THE MODEL for almost all natural growth processes, and it would be extremely surprising if not for the present spread of Covid-19 in given populations. I proved already, that the logistic function described very well the spread in China. So why not in other regions of the world as well.
What is this good for?
One very important property of the logistic function is its symmetry around the turning point x₀. That means, once a spread has been verified to have passed the turning point, we know with a probability approaching certainty how it ends up.
What is Curve Fitting?
We have a Model (here the logistic function consisting of 3 parameters). We have a time series. The curve fitting algorithm iteratively varies the parameters so that the sum of the squares of the differences between each of the simulated values to each data point becomes minimal (least squares method). In said tool, I implemented the Levenberg–Marquardt algorithm as the least squares method.
Why would we care?
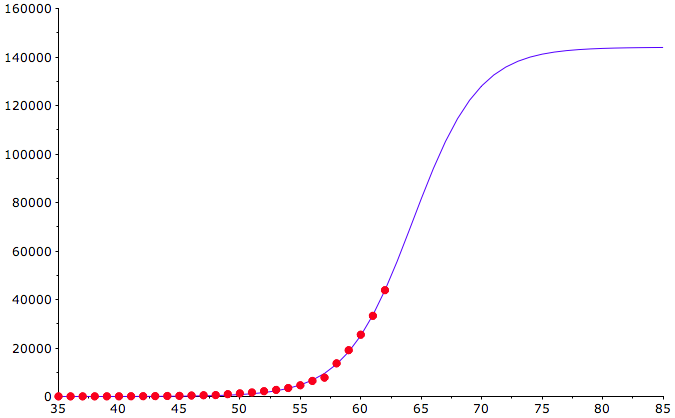
Look at the results of the curve fit of the LF to yesterday's US data according to the JHU/CSSE time series - https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data
Parameter a ist the limiting value, however, since in the US we didn't reach the turning point yet (parameter c = day 64, i.e. March, 25th), the prevision of the limiting value = 144036 confirmed Covid-19 infections is yet a bit uncertain.
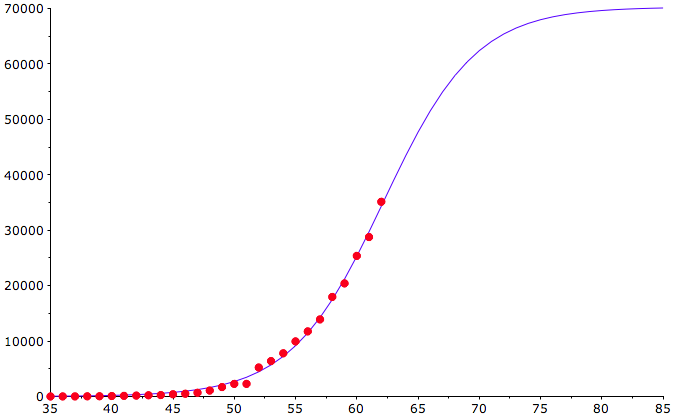
Now, you want to know, how your country is doing, for example Spain?
Turning point was yesterday. In case there are no bigger changes in the containment measures, the spread in Spain will end up with more than 70k confirmed infections in apprx. 2 to 3 weeks.
I follow the time series for Germany, Italy and Brazil on my BLog - https://obsigna.com/articles/1584931539.html. Others may want to follow the spread in their country using said tool.
God help us all.
Quick Start
svnlite co https://github.com/cyclaero/xcssecovid.git/trunk xcssecovid cd xcssecovid clang -g0 -O3 -march=native xcssecovid.c -Wno-parentheses -lm -o xcssecovid fetch -qo - https://github.com/CSSEGISandData/COVID-19/raw/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv | ./xcssecovid US - US.tsv cat US.tsv
Code:
# Model: a/(1 + exp(-b·(x - c)))
# a = 144036 ± 13.179 %
# b = 0.364201 ± 2.7248 %
# c = 64.2688 ± 0.8798 %
# ChiSqr = 92220.86
t/d C L
-20 * 0.000000
-19 * 0.000000
-18 * 0.000000
-17 * 0.000000
...
...
-1 * 0.000007
0 * 0.000010
1 1 0.000014
2 1 0.000020
3 2 0.000029
4 2 0.000042
5 5 0.000061
6 5 0.000088
7 5 0.000126
8 5 0.000181
9 5 0.000261
10 7 0.000376
...
...
50 1281 792.802927
51 1663 1138.378834
52 2179 1632.871155
53 2727 2338.647108
54 3499 3342.320651
55 4632 4762.262397
56 6421 6756.478624
57 7783 9528.646839
58 13677 13327.803195
59 19100 18434.120243
60 25489 25120.832956
61 33276 33584.499721
62 43847 43848.254080
63 * 55667.801935
64 * 68495.183556
65 * 81550.592732
66 * 93997.986502
67 * 105148.182477
68 * 114592.002038
69 * 122218.258863
70 * 128143.172369
...
...
80 * 143569.151663
81 * 143711.229374
82 * 143810.103724
83 * 143878.876950
84 * 143926.695982
85 * 143959.937038
86 * 143983.040349
87 * 143999.095772
88 * 144010.252408
89 * 144018.004514
90 * 144023.390792
...
...What the hell is a Logisitc Function?
According to Wikipedia - https://en.wikipedia.org/wiki/Logistic_function:
A logistic function or logistic curve is a common "S" shape (sigmoid curve), with equation:

The logistic function finds applications in a range of fields, including artificial neural networks, biology (especially ecology), biomathematics, chemistry, demography, economics, geoscience, mathematical psychology, probability, sociology, political science, linguistics, and statistics.
As a matter of fact it is THE MODEL for almost all natural growth processes, and it would be extremely surprising if not for the present spread of Covid-19 in given populations. I proved already, that the logistic function described very well the spread in China. So why not in other regions of the world as well.
What is this good for?
One very important property of the logistic function is its symmetry around the turning point x₀. That means, once a spread has been verified to have passed the turning point, we know with a probability approaching certainty how it ends up.
What is Curve Fitting?
We have a Model (here the logistic function consisting of 3 parameters). We have a time series. The curve fitting algorithm iteratively varies the parameters so that the sum of the squares of the differences between each of the simulated values to each data point becomes minimal (least squares method). In said tool, I implemented the Levenberg–Marquardt algorithm as the least squares method.
Why would we care?
Look at the results of the curve fit of the LF to yesterday's US data according to the JHU/CSSE time series - https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data
Parameter a ist the limiting value, however, since in the US we didn't reach the turning point yet (parameter c = day 64, i.e. March, 25th), the prevision of the limiting value = 144036 confirmed Covid-19 infections is yet a bit uncertain.
Now, you want to know, how your country is doing, for example Spain?
fetch -qo - https://github.com/CSSEGISandData/COVID-19/raw/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv | ./xcssecovid Spain - Spain.tsv head Spain.tsv
Code:
# Model: a/(1 + exp(-b·(x - c)))
# a = 70273.9 ± 8.228 %
# b = 0.264668 ± 3.1934 %
# c = 62.172 ± 0.91822 %
# ChiSqr = 129867.3
t/d C L
-20 * 0.000025
-19 * 0.000033
-18 * 0.000043
-17 * 0.000056Turning point was yesterday. In case there are no bigger changes in the containment measures, the spread in Spain will end up with more than 70k confirmed infections in apprx. 2 to 3 weeks.
I follow the time series for Germany, Italy and Brazil on my BLog - https://obsigna.com/articles/1584931539.html. Others may want to follow the spread in their country using said tool.
God help us all.
Last edited: